Data analysis with python
Overview
Teaching: 0 min
Exercises: 0 minQuestions
What is SciPy?
How can I use Scipy?
Objectives
Learn about SciPy for spatio-temporal data analysis
Using SciPy clustering algorithms on spatio-temporal data
SciPy is a Python-based ecosystem of open-source software for mathematics, science, and engineering. In particular, these are some of the core packages:
- NumPy: the fundamental package for numerical computation. It defines the numerical array and matrix types and basic operations on them.
- SciPy library: a collection of numerical algorithms and domain-specific toolboxes, including signal processing, optimization, statistics and much more.
- Matplotlib: a mature and popular plotting package, that provides publication-quality 2D plotting as well as rudimentary 3D plotting
- IPython: a rich interactive interface, letting you quickly process data and test ideas. The IPython notebook works in your web browser, allowing you to document your computation in an easily reproducible form.
- Sympy: for symbolic mathematics and computer algebra.
- pandas: providing high-performance, easy to use data structures.
- nose: a framework for testing Python code.
We won’t cover the usage of all these packages and will only give a few examples that are meaningful when working with spatio-temporal data.
You know some of these packages, for instance NumPy and Matplotlib; we have used them in previous chapters.
We also use partly IPython when using jupyter notebooks. pandas is one of the best options for working with tabular data in Python. The Pandas library provides data structures, produces high quality plots with matplotlib and integrates nicely with other libraries that use NumPy arrays. If you want to know more about pandas, have a look at the following tutorials/Carpentry lessons:
The usage of nose and Sympy are both outside the scope of this lesson.
SciPy
- scipy.cluster Vector quantization / Kmeans
- scipy.constants Physical and mathematical constants
- scipy.fftpack Fourier transform
- scipy.integrate Integration routines
- scipy.interpolate Interpolation
- scipy.io Data input and output
- scipy.linalg Linear algebra routines
- scipy.ndimage n-dimensional image package
- scipy.odr Orthogonal distance regression
- scipy.optimize Optimization
- scipy.signal Signal processing
- scipy.sparse Sparse matrices
- scipy.spatial Spatial data structures and algorithms
- scipy.special Any special mathematical functions
- scipy.stats Statistics
K-Means Clustering of a Satellite Images using Scipy
This part is taken from the excellent blog of Max Köning.
K-means is a widely used method in cluster analysis. However, this method is valid only if a number of assumptions is valid with your dataset:
- k-means assumes the variance of the distribution of each attribute (variable) is spherical;
- all variables have the same variance;
- the prior probability for all k clusters is the same, i.e., each cluster has roughly equal number of observations;
If any one of these 3 assumptions are violated, then k-means will not be correct.
On major decision you have to take when using K-means is to choose the number of clusters a priori. However, as we will see below, this choice is critical and has a strong influence on the results:
Let’s take the following example where we apply K-means for different number of clusters on a netCDF file containing Monthly Average Precipitable Water over Ice-Free Oceans (kg m-2) October 2009:
import netCDF4
import numpy as np
from scipy.cluster.vq import *
from matplotlib import colors as c
import matplotlib.pyplot as plt
%matplotlib inline
f = netCDF4.Dataset('tpw_v07r01_200910.nc4.nc', 'r')
lats = f.variables['latitude'][:]
lons = f.variables['longitude'][:]
pw = f.variables['precipitable_water'][0,:,:]
f.close()
# Flatten image to get line of values
flatraster = pw.flatten()
flatraster.mask = False
flatraster = flatraster.data
# Create figure to receive results
fig = plt.figure(figsize=[20,7])
fig.suptitle('K-Means Clustering')
# In first subplot add original image
ax = plt.subplot(241)
ax.axis('off')
ax.set_title('Original Image\nMonthly Average Precipitable Water\n over Ice-Free Oceans (kg m-2)')
original=ax.imshow(pw, cmap='rainbow', interpolation='nearest', aspect='auto', origin='lower')
plt.colorbar(original, cmap='rainbow', ax=ax, orientation='vertical')
# In remaining subplots add k-means clustered images
# Define colormap
list_colors=['blue','orange', 'green', 'magenta', 'cyan', 'gray', 'red', 'yellow']
for i in range(7):
print("Calculate k-means with ", i+2, " clusters.")
#This scipy code clusters k-mean, code has same length as flattened
# raster and defines which cluster the value corresponds to
centroids, variance = kmeans(flatraster.astype(float), i+2)
code, distance = vq(flatraster, centroids)
#Since code contains the clustered values, reshape into SAR dimensions
codeim = code.reshape(pw.shape[0], pw.shape[1])
#Plot the subplot with (i+2)th k-means
ax = plt.subplot(2,4,i+2)
ax.axis('off')
xlabel = str(i+2) , ' clusters'
ax.set_title(xlabel)
bounds=range(0,i+2)
cmap = c.ListedColormap(list_colors[0:i+2])
kmp=ax.imshow(codeim, interpolation='nearest', aspect='auto', cmap=cmap, origin='lower')
plt.colorbar(kmp, cmap=cmap, ticks=bounds, ax=ax, orientation='vertical')
plt.show()
The netCDF file we used can be freely downloaded at here.
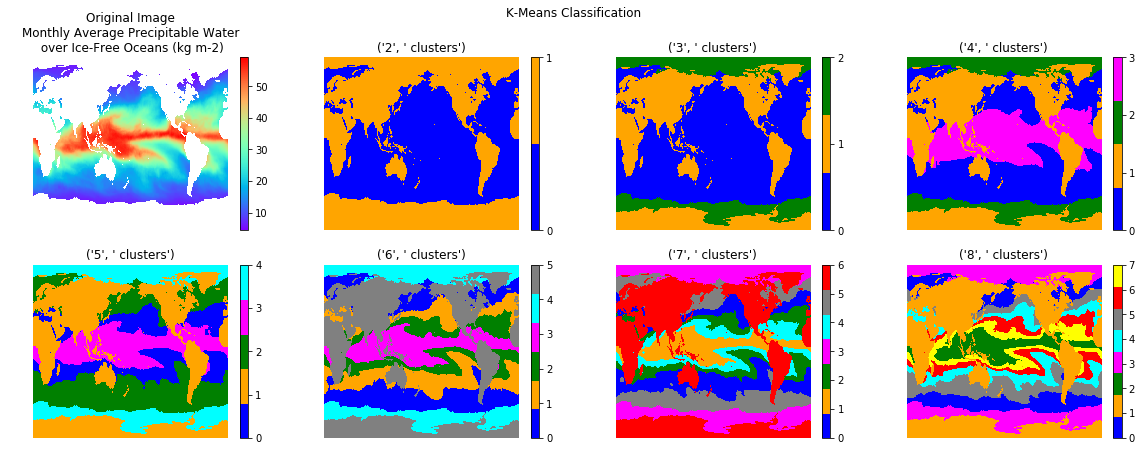
K-means limitations
See here what can happen if you do not choose the “right” number of clusters or when your data do not K-means assumptions.
import netCDF4
import numpy as np
from scipy.cluster.vq import *
from matplotlib import colors as c
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed((1000,2000))
f = netCDF4.Dataset('tpw_v07r01_200910.nc4.nc', 'r')
lats = f.variables['latitude'][:]
lons = f.variables['longitude'][:]
pw = f.variables['precipitable_water'][0,:,:]
f.close()
# Flatten image to get line of values
flatraster = pw.flatten()
flatraster.mask = False
flatraster = flatraster.data
# In first subplot add original image
fig, (ax1, ax2, ax3) = plt.subplots(3, sharex=True)
# Create figure to receive results
fig.set_figheight(20)
fig.set_figwidth(15)
fig.suptitle('K-Means Clustering')
ax1.axis('off')
ax1.set_title('Original Image\nMonthly Average Precipitable Water\n over Ice-Free Oceans (kg m-2)')
original=ax1.imshow(pw, cmap='rainbow', interpolation='nearest', aspect='auto', origin='lower')
plt.colorbar(original, cmap='rainbow', ax=ax1, orientation='vertical')
# In remaining subplots add k-means clustered images
# Define colormap
list_colors=['blue','orange', 'green', 'magenta', 'cyan', 'gray', 'red', 'yellow']
print("Calculate k-means with 6 clusters.")
#This scipy code classifies k-mean, code has same length as flattened
# raster and defines which cluster the value corresponds to
centroids, variance = kmeans(flatraster.astype(float), 6)
code, distance = vq(flatraster, centroids)
#Since code contains the clustered values, reshape into SAR dimensions
codeim = code.reshape(pw.shape[0], pw.shape[1])
#Plot the subplot with 4th k-means
ax2.axis('off')
xlabel = '6 clusters'
ax2.set_title(xlabel)
bounds=range(0,6)
cmap = c.ListedColormap(list_colors[0:6])
kmp=ax2.imshow(codeim, interpolation='nearest', aspect='auto', cmap=cmap, origin='lower')
plt.colorbar(kmp, cmap=cmap, ticks=bounds, ax=ax2, orientation='vertical')
#####################################
thresholded = np.zeros(codeim.shape)
thresholded[codeim==3]=1
thresholded[codeim==5]=2
#Plot only values == 5
ax3.axis('off')
xlabel = 'Keep the fifth cluster only'
ax3.set_title(xlabel)
bounds=range(0,2)
cmap = c.ListedColormap(['white', 'green', 'cyan'])
kmp=ax3.imshow(thresholded, interpolation='nearest', aspect='auto', cmap=cmap, origin='lower')
plt.colorbar(kmp, cmap=cmap, ticks=bounds, ax=ax3, orientation='vertical')
plt.show()
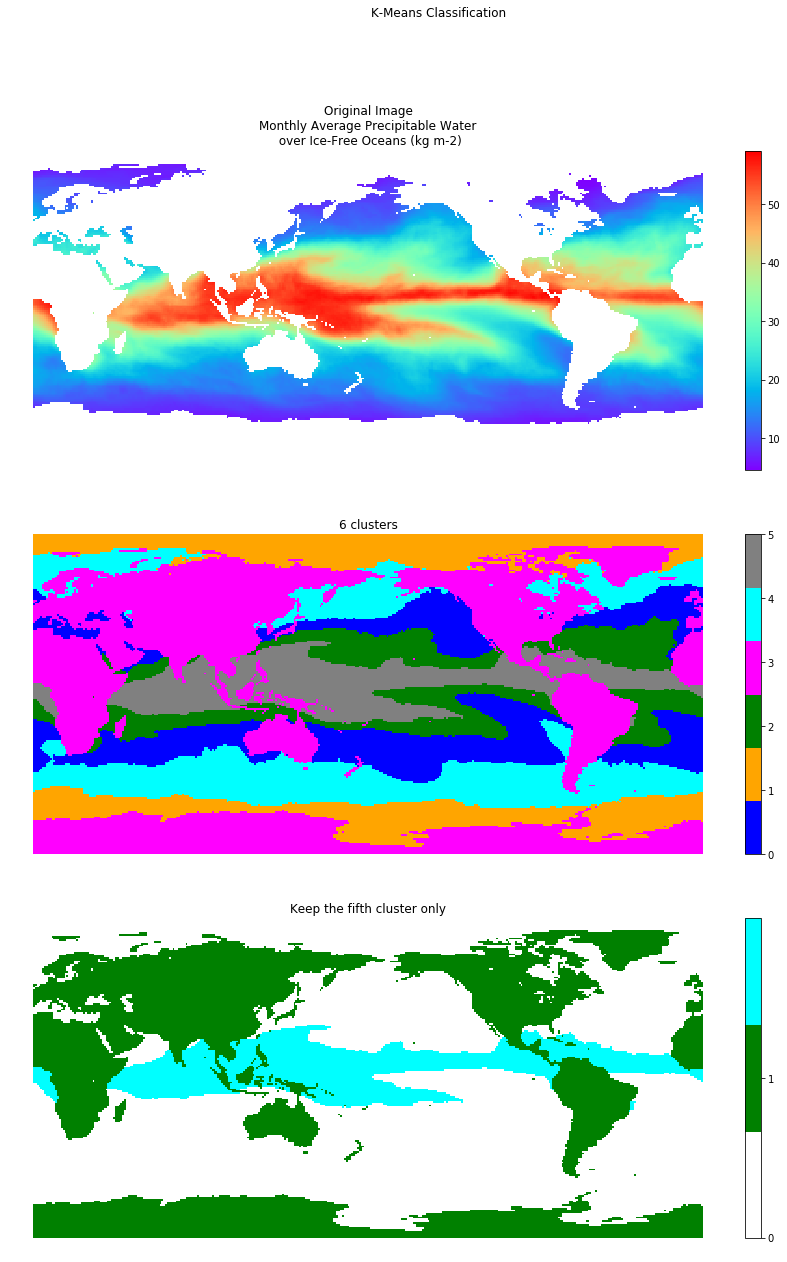
%matplotlib inline
from scipy.spatial import distance
import numpy as np
import matplotlib.pyplot as plt
from skimage import measure
# Find contours at a constant value of 2.0
contours = measure.find_contours(thresholded, 1.0)
# Display the image and plot all contours found
fig = plt.figure(figsize=[20,7])
ax = plt.subplot()
ax.set_title('Original Image\nMonthly Average Precipitable Water\n over Ice-Free Oceans (kg m-2)')
original=ax.imshow(pw, cmap='rainbow', interpolation='nearest', aspect='auto', origin='lower')
plt.colorbar(original, cmap='rainbow', ax=ax, orientation='vertical')
for n, contour in enumerate(contours):
dists = distance.cdist(contour, contour, 'euclidean')
if dists.max() > 200:
ax.plot(contour[:, 1], contour[:, 0], linewidth=2, color='black')
print(dists.max())
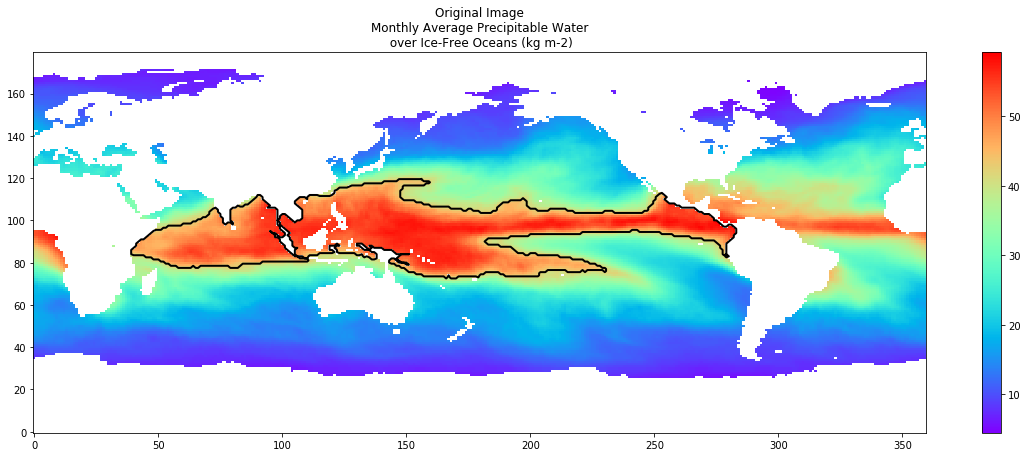
Save contours in a shapefile
To save the resulting contours, we need to get the coordinates of each point of the contour and create a polygon. We start from the preceding code and add
the computation of the coordinates in lat/lon and store them in a shapefile, using shapely and geopandas python packages:
%matplotlib inline
from scipy.spatial import distance
import numpy as np
import matplotlib.pyplot as plt
from skimage import measure
import geopandas as gpd
from fiona.crs import from_epsg
from shapely import geometry
# Find contours at a constant value of 2.0
contours = measure.find_contours(thresholded, 1.0)
# Create an empty geopandas GeoDataFrame
newdata = gpd.GeoDataFrame()
# Create a new column called 'geometry' to the GeoDataFrame
newdata['geometry'] = None
# Set the GeoDataFrame's coordinate system to WGS84
newdata.crs = from_epsg(4326)
# Display the image and plot all contours found
fig = plt.figure(figsize=[20,7])
ax = plt.subplot()
ax.set_title('Original Image\nMonthly Average Precipitable Water\n over Ice-Free Oceans (kg m-2)')
original=ax.imshow(pw, cmap='rainbow', interpolation='nearest', aspect='auto', origin='lower')
plt.colorbar(original, cmap='rainbow', ax=ax, orientation='vertical')
ncontour=0
for n, contour in enumerate(contours):
dists = distance.cdist(contour, contour, 'euclidean')
if dists.max() > 200:
ax.plot(contour[:, 1], contour[:, 0], linewidth=2, color='black')
# Approximate latitudes/longitudes of the contour
coords = []
for c in contour:
if int(c[0]) == c[0]:
lat = lats[int(c[ 0])]
else:
lat = (lats[int(c[ 0])] + lats[int(c[0])+1])/2.0
if int(c[1]) == c[1]:
lon = lons[int(c[ 1])]
else:
lon = (lons[int(c[ 1])] + lons[int(c[1])+1])/2.0
coords.append([lon,lat])
poly = geometry.Polygon([[c[0], c[1]] for c in coords])
newdata.loc[ncontour, 'geometry'] = poly
newdata.loc[ncontour,'idx_name'] = 'contour_' + str(ncontour)
print(ncontour)
print(dists.max())
ncontour += 1
# Write the data into that Shapefile
newdata.to_file("contour_test.shp")
Then we can plot it:
%matplotlib inline
from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt
fig = plt.figure(figsize=[12,15]) # a new figure window
ax = fig.add_subplot(1, 1, 1) # specify (nrows, ncols, axnum)
map = Basemap(projection='cyl',llcrnrlat=-90,urcrnrlat=90,\
llcrnrlon=0,urcrnrlon=360,resolution='c')
map.drawmapboundary(fill_color='aqua')
map.fillcontinents(color='#ffe2ab',lake_color='aqua')
map.drawcoastlines()
contour_test= map.readshapefile('contour_test', 'contour_test', linewidth=2.0, color="red")
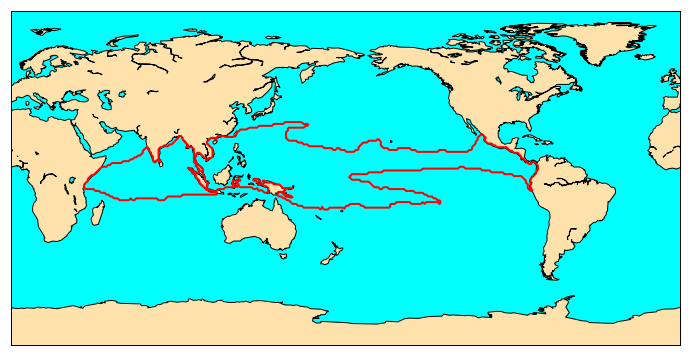
Key Points
scipy library